最近看看JPEG编码原理,里面用到了哈夫曼(huffman)编码,查询资料加上个人理解总结了下。我们先来看下这个问题:例:将学生的百分制成绩转换为五分制成绩:≥90 分: Ab+树,80~89分: Bb+树,70~79分: C,60~69分: D,<60分: E。
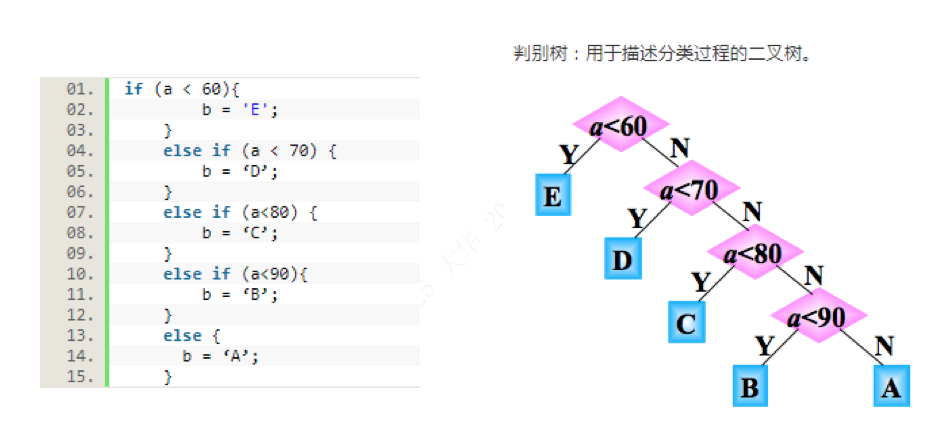
成绩判断逻辑
如上图所述,为常用的判断逻辑,根据输入的分数找到对应分支。在此基础上,如果考虑到程序的执行效率,假设对应分数段和该分数段出现的概率是一样的。那么使用如上判断逻辑方案一,比如学生的总成绩数据有10000条,则5%的数据需要 1 次比较,15%的数据需 2 次比较,40%的数据需 3 次比较,40%的数据需 4 次比较,因此 10000 个数据比较的次数:10000× (5%+2×15%+3×40%+4×40%)=31500次。
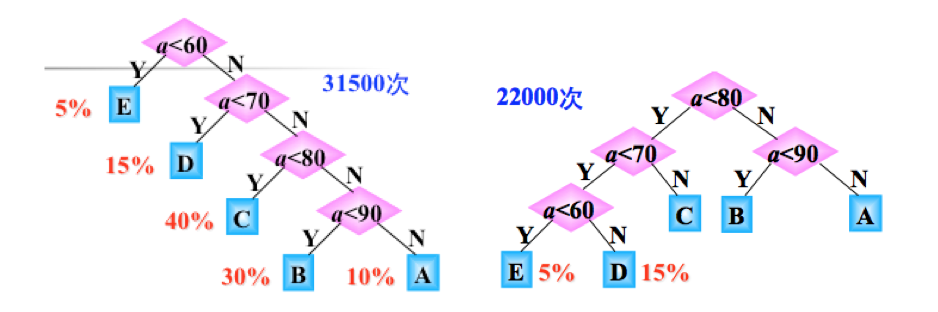
不同逻辑执行时间
假如使用方案二,此种形状的二叉树,需要的比较次数是:10000× (3×5%+3×15%+2×40%+ 2×10%+ 2×30%)=22000次。
显然:两种判别树的效率是不一样的。
那么能不能有办法找到一种效率最高的树呢?此时引出了哈夫曼(huffman)树;
我们先来理解下相关的概念:
路径:若树中存在一个结点序列k1,k2,…,kj,使得ki是ki+1的双亲,则称该结点序列是从k1到kj的一条路径。
路径长度:等于路径上的结点数减1。
结点的权:在许多应用中,常常将树中的结点赋予一个有意义的数,称为该结点的权。
结点的带权路径长度:是指该结点到树根之间的路径长度与该结点上权的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和,通常记作:
n表示叶子结点的数目,Wi和Li分别表示叶子结点Ki的权值和树根结点到叶子结点Ki之间的路径长度。
哈夫曼树(huffman树)定义:在权为w1,w2,…,wn的n个叶子结点的所有二叉树中,带权路径长度WPL最小的二叉树称为哈夫曼树或最优二叉树。例:有4 个结点 a, b, c, d,权值分别为 7, 5, 2, 4,试构造以此 4 个结点为叶子结点的二叉树。
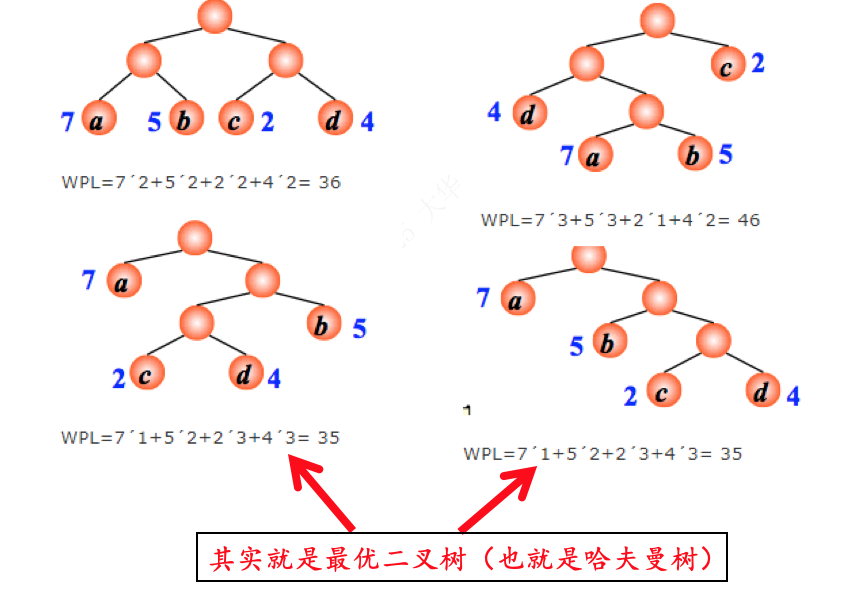
哈夫曼树介绍
那么如果高效的构建一颗哈夫曼树呢?使用哈夫曼算法;
1.根据给定的n个权值{w1,w2,…,wn}构成二叉树集合F={T1,T2,…,Tn},其中每棵二叉树Ti中只有一个带权为wi的根结点,其左右子树为空;
2.在F中选取两棵根结点权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为左右子树根结点的权值之和;
3.在F中删除这两棵树,同时将新的二叉树加入F中;
4.重复2、3,直到F只含有一棵树为止,得到哈夫曼树。
算法描述有点抽象,接下来我们使用一个实例来理解一下:例:有4 个节点 A,B,C,D,权值分别为 7, 5, 2, 4,构造哈夫曼树。这里为了表述简洁,直接用图片标注方式表述构造过程:
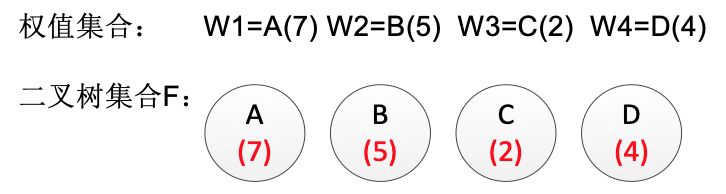
给定的节点和权
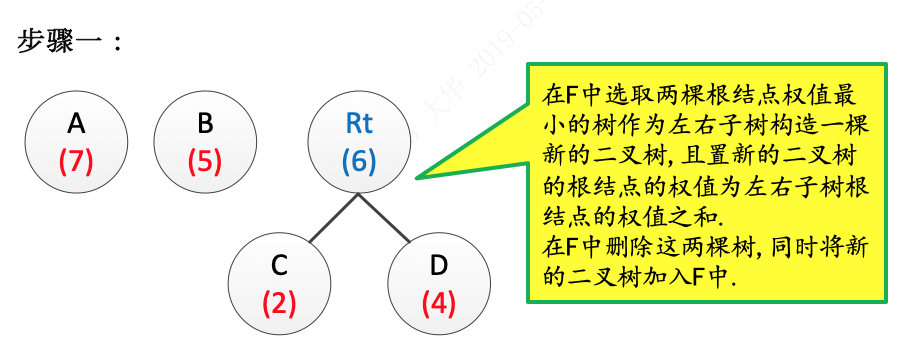
步骤一
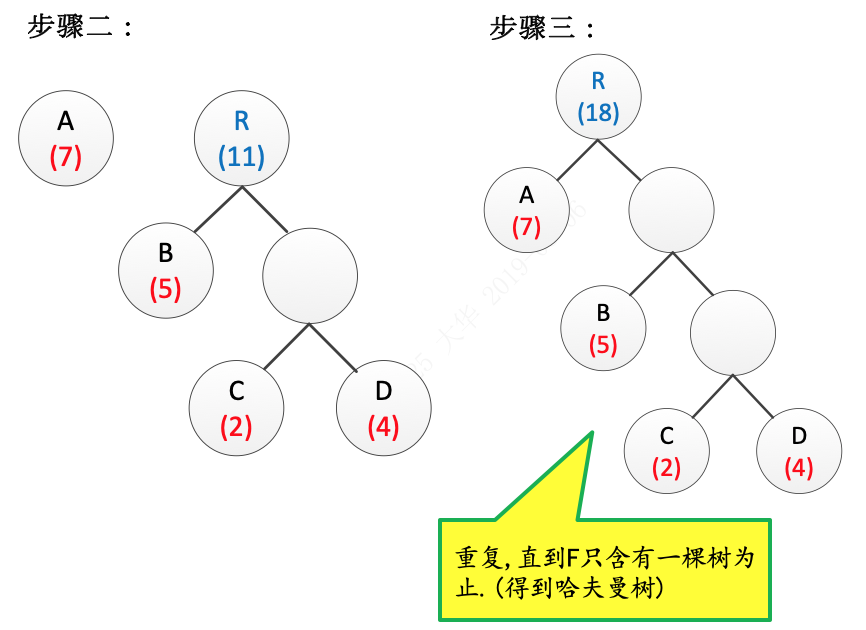
步骤二和步骤三
关于哈夫曼树的注意点:1、满二叉树不一定是哈夫曼树
2、哈夫曼树中权越大的叶子离根越近 (很好理解,WPL最小的二叉树)
3、具有相同带权结点的哈夫曼树不惟一
4、哈夫曼树的结点的度数为 0 或 2, 没有度为 1 的结点。
5、包含 n 个叶子结点的哈夫曼树中共有 2n – 1 个结点。
6、包含 n 棵树的森林要经过 n–1 次合并才能形成哈夫曼树,共产生 n–1 个新结点
哈夫曼树就介绍到这里,下一篇继续介绍哈夫曼树的应用—哈夫曼编码。
限时特惠:本站每日持续更新海量展厅资源,一年会员只需29.9元,全站资源免费下载
站长微信:zhanting688





