关于二叉树的内容,我觉得二叉树最核心的地方就是它的几种遍历方式,基本上所有的问题都是围绕着几种遍历方式来的。因此就在这总结一下这几种遍历方式。
前序遍历
一、简介
前序遍历(DLR),是二叉树遍历的一种,也叫做先根遍历、先序遍历,可记做根左右。
前序遍历首先访问根结点然后遍历左子树,最后遍历右子树。在遍历左、右子树时,仍然先访问根结点前序遍历中序遍历后序遍历,然后遍历左子树,最后遍历右子树。
若二叉树为空则结束返回,否则:
1.访问根结点
2.前序遍历左子树
2.前序遍历右子树
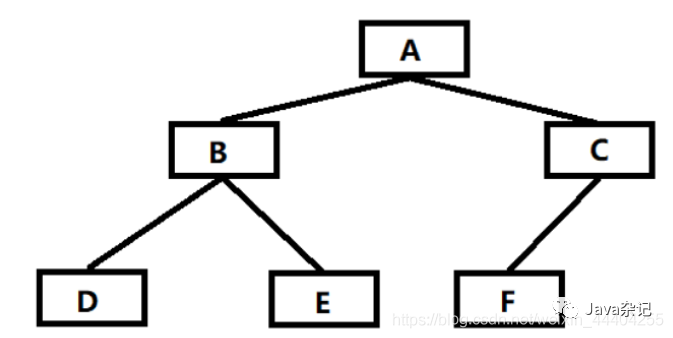
如图:前序遍历结果:ABDECF
二、代码实现
1.递归实现
class TreeNode{//TreeNode类,后边同样TreeNode left;TreeNode right;int val;TreeNode(int val){this.val = val;}}
public class PreOrderTraversal {public void preOrder(TreeNode root){if(root != null){System.out.println(root.val);//打印根节点preOrder(root.left);//访问左子树preOrder(root.right);//访问右子树}}}
2.非递归实现
方法一:根节点存入栈中打印根节点,然后访问这个根节点的左子树,左子树也是将左子树的根存入栈中打印根节点,依次往下直到左子树为空,再取出栈顶元素,栈顶元素(访问完左子树的根节点)作为新的根节点去访问右子树。
public void preorderTraversal(TreeNode root) {Stack stack = new Stack();//用一个栈来存放树中的节点while(root != null || !stack.isEmpty()) {//只要当前节点不为空(即当前节点的左右子树没有访问完毕)或者栈中还有节点(还有节点没有访问)while (root != null) {//一直往左走stack.push(root);//根节点入栈System.out.println(root.val);//打印根节点root = root.left;//访问左子树}root = stack.pop();//取出根节点root = root.right;//访问右子树}}
方法二:我们知道前序遍历遵从根左右的顺序,所以我们打印根节点,并将它的右子树,左子树按照顺序压入栈中,每次只取出栈顶的一个节点,这样就可以保证所有的左子树都会在右子树之前取出并打印。
import java.util.Stack;public class PreOrderTraversal {public void preorderTraversal(TreeNode root) {Stack stack = new Stack();if(root == null)//树为空return;stack.add(root);//将根节点压入栈中while(!stack.isEmpty()){//只要栈不为空,执行循环TreeNode node = stack.pop();//取出栈顶元素打印,此时的栈顶元素是以node为根的子树的根System.out.println(node.val);if(node.right != null)//将右子树压入栈中stack.push(node.right);if(node.left != null)//将左子树压入栈中stack.push(node.left);}}}
中序遍历
一、简介
中序遍历(LDR)是二叉树遍历的一种,也叫做中根遍历、中序周游。可记做左根右
中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。
若二叉树为空则结束返回,否则:
1.中序遍历左子树
2.访问根结点
3.中序遍历右子树
如图:中序遍历结果:DBEAFC
二、代码实现
1.递归实现
public class InOrderTraversal {public void inorderTraversal(TreeNode root){if(root != null){inorderTraversal(root.left);//访问左子树System.out.println(root.val);//打印根节点inorderTraversal(root.right);//访问右子树}}}
2.非递归实现
根前序遍历方法一思路一样,不同的只是先不打印根节点,而是先访问左子树,再打印根节点,访问右子树。
import java.util.Stack;public class InOrderTraversal {public void inorderTraversal(TreeNode root){Stack stack = new Stack();while(root != null || !stack.isEmpty()){//只要当前节点不为空(即当前节点的左右子树没有访问完毕)或者栈中还有节点(还有节点没有访问)while(root != null){stack.push(root);//根节点入栈root = root.left;//访问左子树}root = stack.pop();//取出左子树的根节点System.out.println(root.val);//打印根节点root = root.right;//访问右子树}}}
后序遍历
一、简介
首先遍历左子树,然后遍历右子树,最后遍历访问根结点,在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后遍历根结点。
若二叉树为空则结束返回,否则:
1.中序遍历左子树
2.中序遍历右子树
3.访问根结点
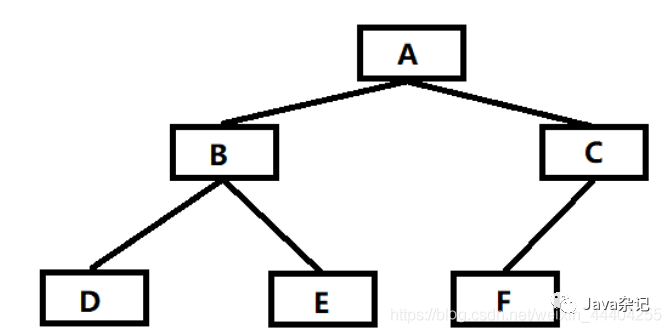
如图:后序遍历结果:DEBFCA
二、代码实现
1.递归实现
public class PostOrderTraversal {public void postOrder(TreeNode root){if(root != null){postOrder(root.left);//访问左子树postOrder(root.right);//访问右子树System.out.println(root.val);//打印根节点}}}
2.非递归实现
方法一:常规遍历左右根,和前序、中序方法一类似。
import java.util.Stack;public class PostOrderTraversal {public void postorderTraversal(TreeNode root) {Stack stack = new Stack();TreeNode node = root;TreeNode prev = null;while(node != null || !stack.isEmpty()){while(node != null){//访问左子树stack.push(node);node = node.left;}//判断栈顶元素(根)node = stack.peek();//1.如果此时的根的右子树为空node.right == null//2.如果此时的根的右子树已经访问过了node.right == prev(prev记录的是上次访问打印的节点)if(node.right == null || node.right == prev){//打印根节点,并出栈,将打印过的节点从栈中删除stack.pop();System.out.println(node.val);//记录prev,表示以当前prev为根的子树已经访问过了prev = node;//node置null就不会再次访问以node为根节点的左右子树,这里的node既然已经打印,说明它的左右子树早已访问完毕node = null;}else{//访问右子树node = node.right;}}}}
方法二:和前序遍历的方法二类似,我们可以用一个线性表存放后序遍历的结果。我们知道后序遍历是左右根,但是我们可以反过来,一样先访问根,只是将根放在后边然后访问右子树放在根的前边左子树的后边,我们可以用线性表头插来实现这个操作,先访问根再右子树再左子树,只是每次都对线性表进行头插,这样最后的结果就还是左右根。
import java.util.LinkedList;import java.util.List;import java.util.Stack;public class PostOrderTraversal {public List postorderTraversal(TreeNode root) {Stack stack = new Stack();List list = new LinkedList();if(root == null)return list;stack.push(root);while(!stack.isEmpty()){TreeNode node = stack.pop();list.add(0, node.val);//头插此时根节点if(node.left != null)stack.push(node.left);if(node.right != null)stack.push(node.right);}return list;}}
层序遍历
一、简介
除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推前序遍历中序遍历后序遍历,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
如图:层序遍历结果:ABCDEF

二、代码实现
import java.util.LinkedList;import java.util.Queue;public class LevelOrder {public void levelOrder(TreeNode root) {Queue queue = new LinkedList();if(root != null){//如果根节点不为空,将第一层根节点入队列queue.offer(root);}while(!queue.isEmpty()){//只要队列不为空,执行循环int num = queue.size();//记录此时队列的长度,此时的num代表了某一层一共有多少个节点,防止被后边入队的节点个数影响输出这一层的节点for(int i = 0; i < num; i++){//对某一层的所有节点进行操作(从左到右)TreeNode topNode = queue.poll();//取出这一层第一个节点System.out.println(topNode.val);//打印节点if(topNode.left != null){//将此节点的左子树根节点入队列queue.offer(topNode.left);}if(topNode.right != null){//将此节点的右子树根节点入队列queue.offer(topNode.right);}}}}}
总结:
所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问 题。遍历是二叉树上最重要的运算之一,是二叉树上进行其它运算之基础。一定要仔细体会其中的遍历过程。
限时特惠:本站每日持续更新海量展厅资源,一年会员只需29.9元,全站资源免费下载
站长微信:zhanting688




