前序遍历-图解「剑指Offer」之用前序和中序遍历序列构建二叉树

点击蓝色“五分钟学算法”关注我哟

加个“星标”，天天中午 12:15，一起学算法

吴涟序整容前照片_前言和序言的顺序_前序遍历

作者 |程序员小吴

来源 | 五分钟学算法

题目描述

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:

你可以假设树中没有重复的元素。

例如前序遍历前序遍历，给出

前序遍历 preorder = [28，16，13，22，30，29，43]
中序遍历 inorder = [13，16，22，28，29，30，43]

返回如下的二叉树：

         28
       /    
     16     30
    /      /  
   13  22  29  43

题目解析

先来了解一下前序遍历、中序遍历、后序遍历是什么。

前序遍历：遍历顺序为父（根）节点 -> 左子节点 -> 右子节点

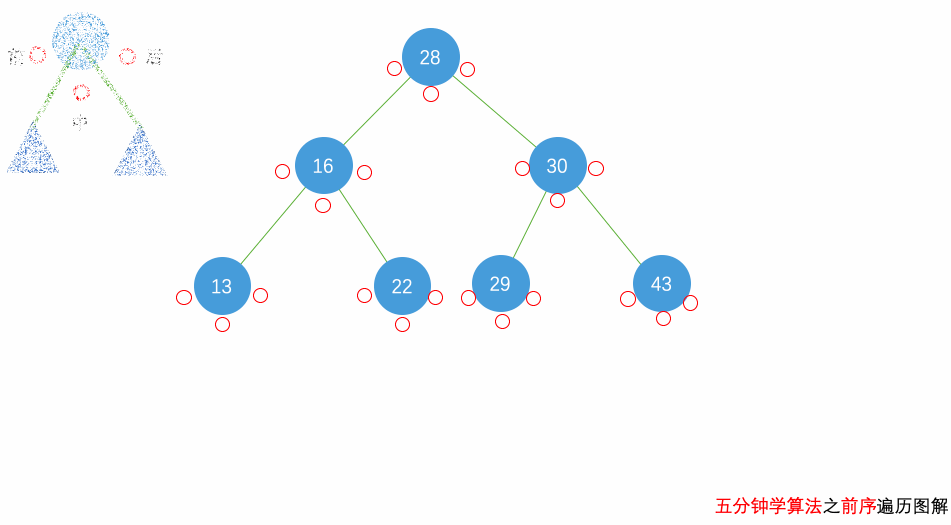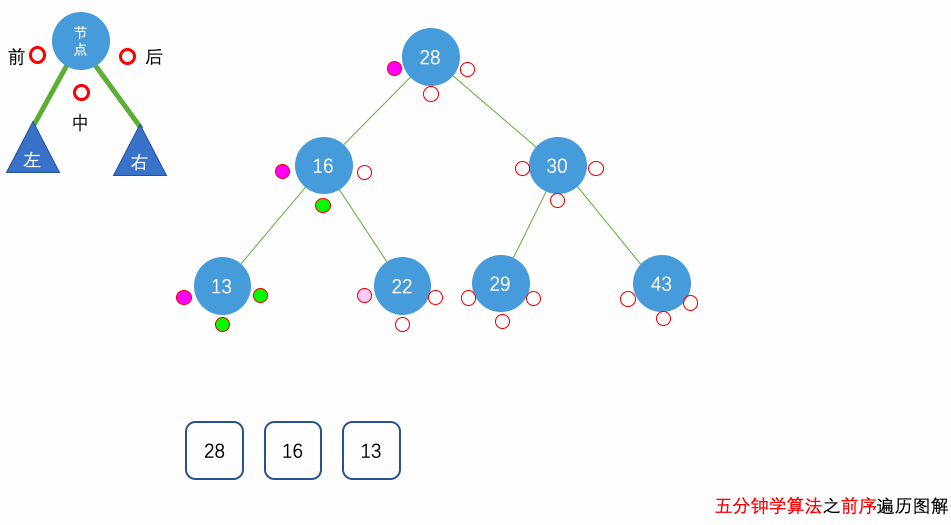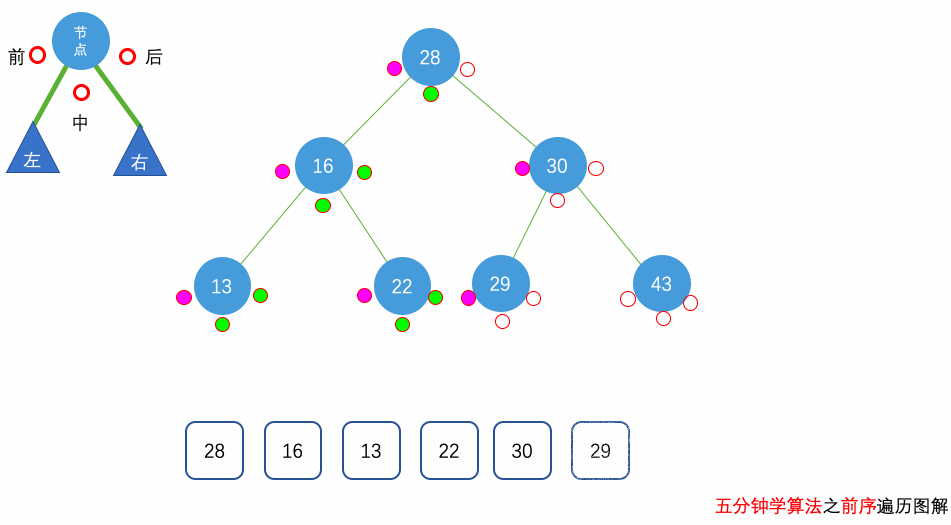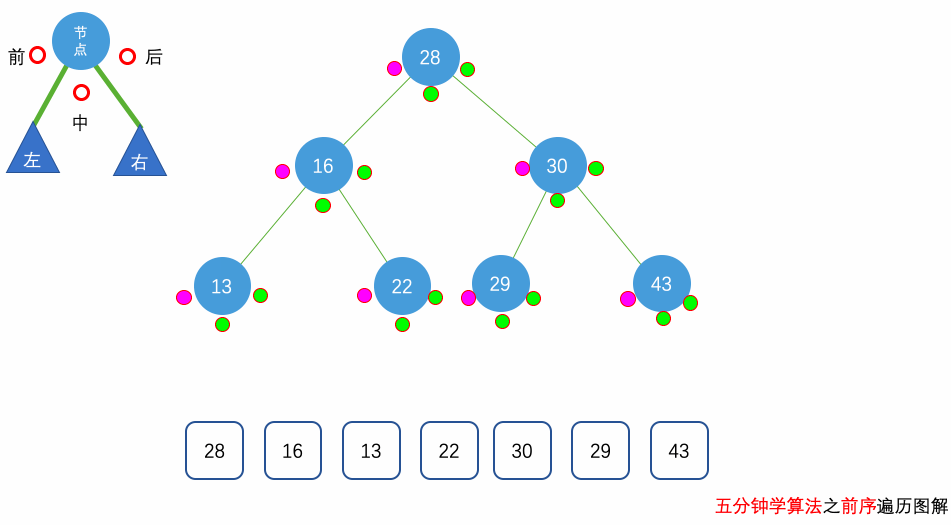
前序遍历_前言和序言的顺序_吴涟序整容前照片

中序遍历：遍历顺序为左子节点 -> 父（根）节点 -> 右子节点

后序遍历：遍历顺序为左子节点 -> 右子节点 -> 父（根）节点

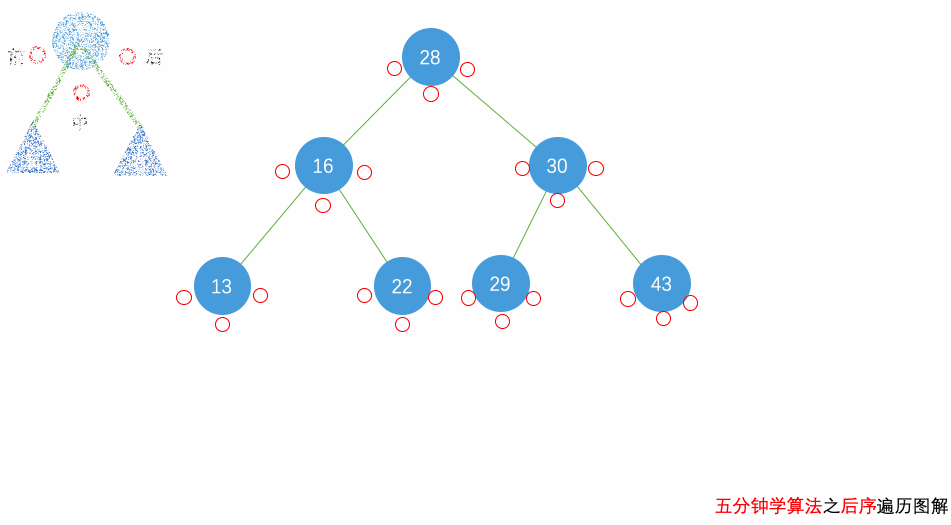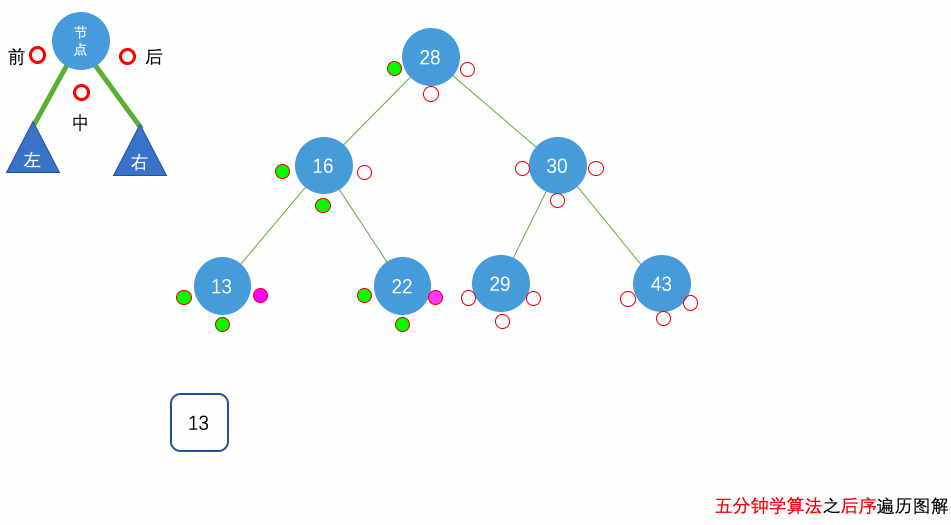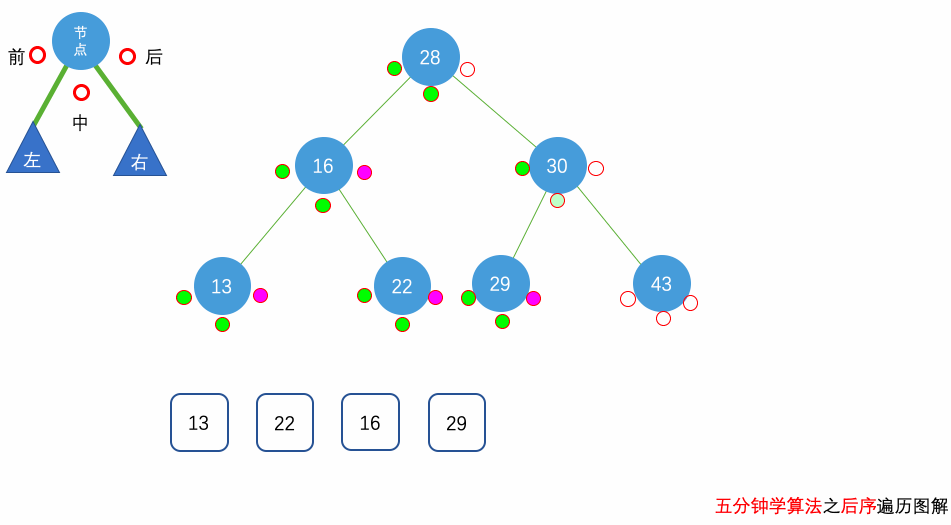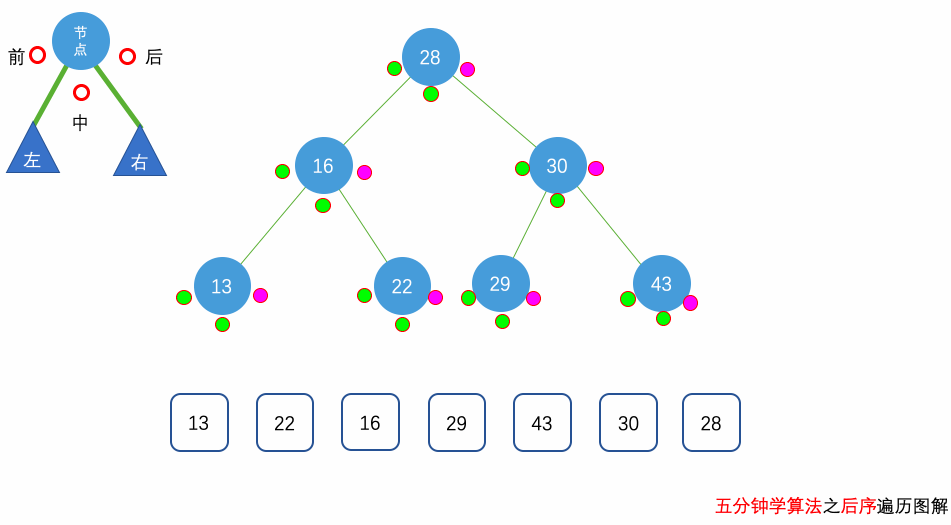
前言和序言的顺序_吴涟序整容前照片_前序遍历

再说明一个结论：前序/后序 + 中序遍历可以确定一棵唯一二叉树。

题目中给出的是前序 + 中序的组合，那么我们仔细观察对比一下 前序遍历 与中序遍历。

如果我们要递归生成二叉树的话，下一层递归应该是：

两个注意点：

动画描述

图片描述

代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
//author:程序员小吴
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
       //借助哈希表来储存二叉树的节点，优化时间复杂度
       Map inPos = new HashMap();
       for (int i = 0; i < inorder.length; ++i){
            inPos.put(inorder[i], i);
       }
       return buildTree(preorder, 0, preorder.length-1, 0, inPos);
    }

    private TreeNode buildTree( int[] pre, int preStart , int preEnd, int inStart, Map inPos) {
    //递归停止条件
    if (preStart > preEnd) return null; 
    //前序中左起第一位肯定是根结点
    TreeNode root = new TreeNode(pre[preStart]);
    //根结点的位置直接通过中序获取
    int rootIdx = inPos.get(pre[preStart]);
    //左子树结点个数可以通过中序中根节点的位置与中序中起始位置确定
    int leftLen = rootIdx - inStart;
    //递归调用
    root.left = buildTree(pre, preStart + 1, preStart + leftLen, inStart, inPos);
    root.right = buildTree(pre, preStart + leftLen + 1, preEnd, rootIdx + 1, inPos);
    return root;
  }
}

复杂度分析知识点

二叉树、递归

相关文章